In an Autoregressive Model How Do You Know if You Should Remove Any Variables
Autoregression Models for Time Series Forecasting With Python
Last Updated on September vii, 2021
Autoregression is a time serial model that uses observations from previous fourth dimension steps as input to a regression equation to predict the value at the next time step.
It is a very simple idea that tin result in accurate forecasts on a range of time series issues.
In this tutorial, you will find how to implement an autoregressive model for fourth dimension series forecasting with Python.
After completing this tutorial, you lot volition know:
- How to explore your time serial data for autocorrelation.
- How to develop an autocorrelation model and employ it to make predictions.
- How to use a developed autocorrelation model to make rolling predictions.
Boot-start your project with my new book Time Series Forecasting With Python, including step-by-pace tutorials and the Python source code files for all examples.
Let's go started.
- Updated May/2017: Fixed minor typo in autoregression equation.
- Updated Apr/2019: Updated the link to dataset.
- Updated Aug/2019: Updated data loading to use new API.
- Updated Sep/2019: Updated examples to use latest plotting API.
- Updated April/2020: Inverse AR to AutoReg due to API change.
Autoregression Models for Fourth dimension Serial Forecasting With Python
Photo by Umberto Salvagnin, some rights reserved.
Autoregression
A regression model, such as linear regression, models an output value based on a linear combination of input values.
For example:
Where yhat is the prediction, b0 and b1 are coefficients establish by optimizing the model on grooming information, and X is an input value.
This technique can exist used on time series where input variables are taken as observations at previous time steps, called lag variables.
For instance, we can predict the value for the next time step (t+i) given the observations at the last two time steps (t-i and t-2). As a regression model, this would look as follows:
| X(t+1) = b0 + b1*X(t-ane) + b2*X(t-2) |
Because the regression model uses information from the aforementioned input variable at previous time steps, information technology is referred to as an autoregression (regression of self).
End learning Time Serial Forecasting the slow way!
Take my free 7-day e-mail course and discover how to become started (with sample code).
Click to sign-up and likewise get a gratis PDF Ebook version of the course.
Autocorrelation
An autoregression model makes an assumption that the observations at previous fourth dimension steps are useful to predict the value at the next time step.
This relationship between variables is called correlation.
If both variables change in the aforementioned direction (e.g. become up together or down together), this is called a positive correlation. If the variables move in reverse directions as values alter (e.g. i goes up and ane goes down), so this is called negative correlation.
We can use statistical measures to summate the correlation between the output variable and values at previous time steps at various different lags. The stronger the correlation between the output variable and a specific lagged variable, the more weight that autoregression model tin can put on that variable when modeling.
Once more, because the correlation is calculated betwixt the variable and itself at previous time steps, it is called an autocorrelation. It is besides called series correlation because of the sequenced structure of time series information.
The correlation statistics can also help to choose which lag variables will be useful in a model and which will not.
Interestingly, if all lag variables show low or no correlation with the output variable, and then it suggests that the time series problem may not be predictable. This tin can exist very useful when getting started on a new dataset.
In this tutorial, we will investigate the autocorrelation of a univariate time series then develop an autoregression model and apply information technology to make predictions.
Before we do that, let'southward first review the Minimum Daily Temperatures data that will be used in the examples.
Minimum Daily Temperatures Dataset
This dataset describes the minimum daily temperatures over 10 years (1981-1990) in the city Melbourne, Australia.
The units are in degrees Celsius and at that place are 3,650 observations. The source of the information is credited as the Australian Bureau of Meteorology.
- Download the dataset.
Download the dataset into your electric current working directory with the filename "daily-min-temperatures.csv".
The code below will load the dataset as a Pandas Series.
| from pandas import read_csv from matplotlib import pyplot serial = read_csv ( 'daily-min-temperatures.csv' , header = 0 , index_col = 0 ) impress ( serial . head ( ) ) series . plot ( ) pyplot . testify ( ) |
Running the example prints the get-go 5 rows from the loaded dataset.
| Engagement 1981-01-01 20.seven 1981-01-02 17.9 1981-01-03 18.8 1981-01-04 14.6 1981-01-05 xv.8 Proper name: Temp, dtype: float64 |
A line plot of the dataset is then created.
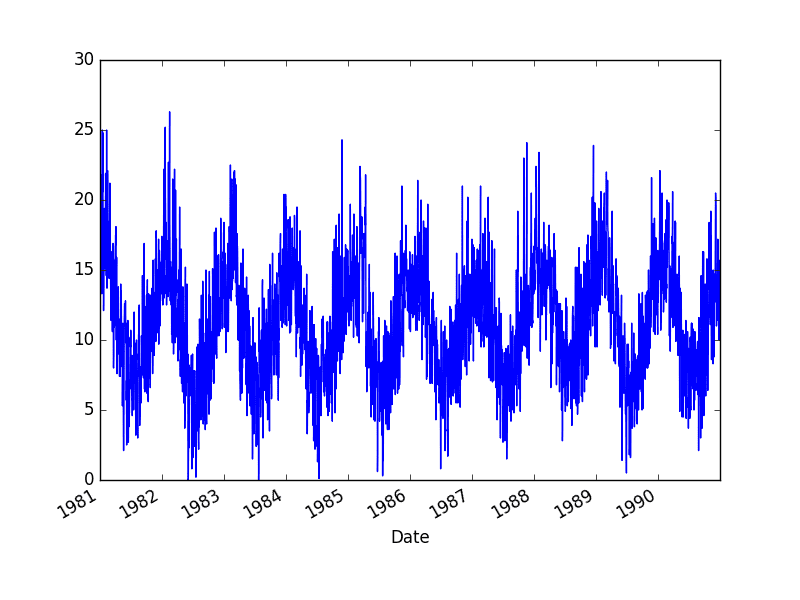
Minimum Daily Temperature Dataset Plot
Quick Check for Autocorrelation
In that location is a quick, visual check that nosotros can practice to come across if at that place is an autocorrelation in our fourth dimension series dataset.
We tin can plot the observation at the previous fourth dimension stride (t-one) with the ascertainment at the adjacent time footstep (t+1) as a scatter plot.
This could exist done manually by starting time creating a lag version of the time series dataset and using a congenital-in scatter plot function in the Pandas library.
But there is an easier way.
Pandas provides a built-in plot to do exactly this, chosen the lag_plot() office.
Below is an instance of creating a lag plot of the Minimum Daily Temperatures dataset.
| from pandas import read_csv from matplotlib import pyplot from pandas . plotting import lag_plot series = read_csv ( 'daily-min-temperatures.csv' , header = 0 , index_col = 0 ) lag_plot ( series ) pyplot . show ( ) |
Running the example plots the temperature data (t) on the ten-axis against the temperature on the previous day (t-1) on the y-centrality.
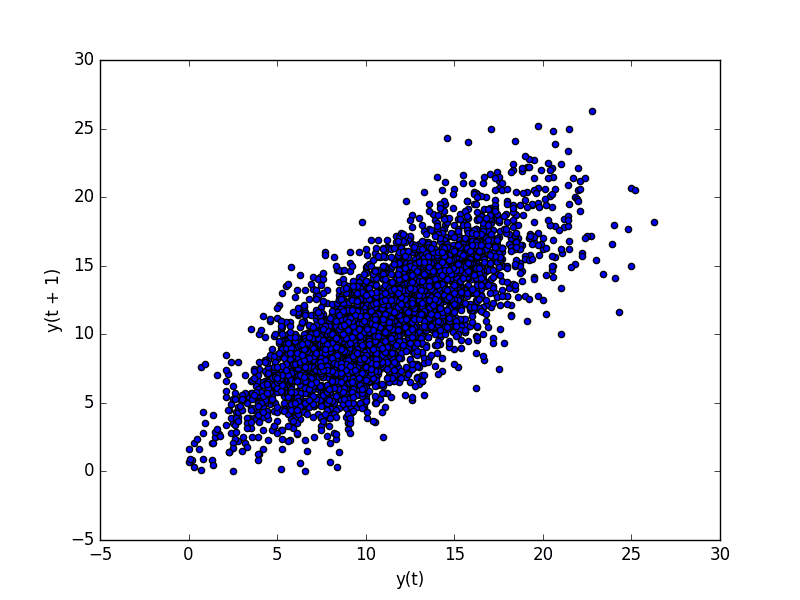
Minimum Daily Temperature Dataset Lag Plot
We tin meet a large ball of observations along a diagonal line of the plot. Information technology clearly shows a relationship or some correlation.
This procedure could be repeated for whatsoever other lagged observation, such equally if we wanted to review the relationship with the last vii days or with the aforementioned twenty-four hour period last month or final year.
Another quick check that nosotros tin do is to direct summate the correlation between the observation and the lag variable.
We can use a statistical test similar the Pearson correlation coefficient. This produces a number to summarize how correlated two variables are betwixt -i (negatively correlated) and +ane (positively correlated) with small values close to zero indicating low correlation and high values to a higher place 0.five or below -0.5 showing loftier correlation.
Correlation tin be calculated easily using the corr() office on the DataFrame of the lagged dataset.
The example below creates a lagged version of the Minimum Daily Temperatures dataset and calculates a correlation matrix of each column with other columns, including itself.
| from pandas import read_csv from pandas import DataFrame from pandas import concat from matplotlib import pyplot series = read_csv ( 'daily-min-temperatures.csv' , header = 0 , index_col = 0 ) values = DataFrame ( series . values ) dataframe = concat ( [ values . shift ( one ) , values ] , axis = i ) dataframe . columns = [ 't-ane' , 't+i' ] result = dataframe . corr ( ) print ( upshot ) |
This is a good confirmation for the plot above.
It shows a strong positive correlation (0.77) between the ascertainment and the lag=1 value.
| t-1 t+1 t-one 1.00000 0.77487 t+ane 0.77487 1.00000 |
This is skillful for one-off checks, but tedious if nosotros desire to check a large number of lag variables in our time series.
Next, nosotros volition look at a scaled-upwardly version of this approach.
Autocorrelation Plots
We tin can plot the correlation coefficient for each lag variable.
This tin very quickly give an idea of which lag variables may be good candidates for use in a predictive model and how the relationship between the observation and its celebrated values changes over time.
We could manually calculate the correlation values for each lag variable and plot the result. Thankfully, Pandas provides a built-in plot called the autocorrelation_plot() office.
The plot provides the lag number along the x-axis and the correlation coefficient value between -1 and 1 on the y-axis. The plot as well includes solid and dashed lines that indicate the 95% and 99% confidence interval for the correlation values. Correlation values above these lines are more than pregnant than those below the line, providing a threshold or cutoff for selecting more than relevant lag values.
| from pandas import read_csv from matplotlib import pyplot from pandas . plotting import autocorrelation_plot series = read_csv ( 'daily-min-temperatures.csv' , header = 0 , index_col = 0 ) autocorrelation_plot ( serial ) pyplot . evidence ( ) |
Running the example shows the swing in positive and negative correlation as the temperature values change across summer and wintertime seasons each previous yr.
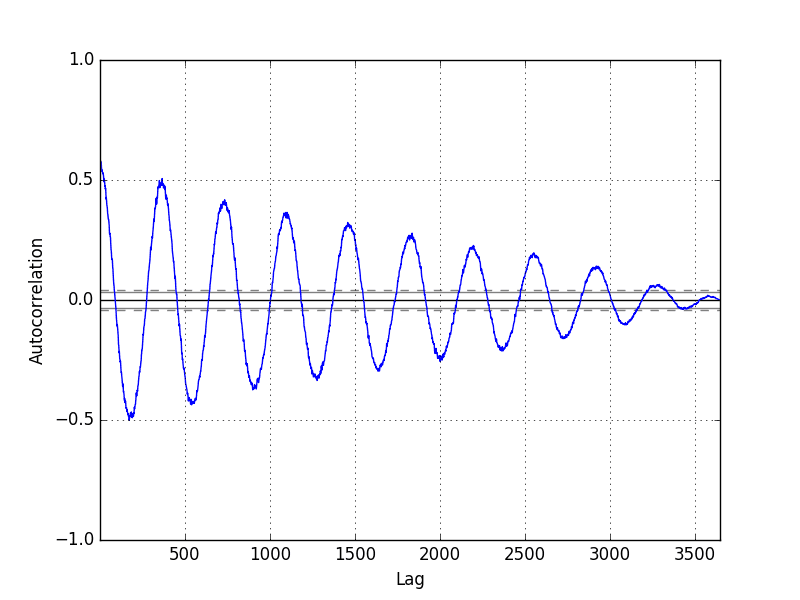
Pandas Autocorrelation Plot
The statsmodels library also provides a version of the plot in the plot_acf() role every bit a line plot.
| from pandas import read_csv from matplotlib import pyplot from statsmodels . graphics . tsaplots import plot_acf serial = read_csv ( 'daily-min-temperatures.csv' , header = 0 , index_col = 0 ) plot_acf ( series , lags = 31 ) pyplot . show ( ) |
In this example, nosotros limit the lag variables evaluated to 31 for readability.
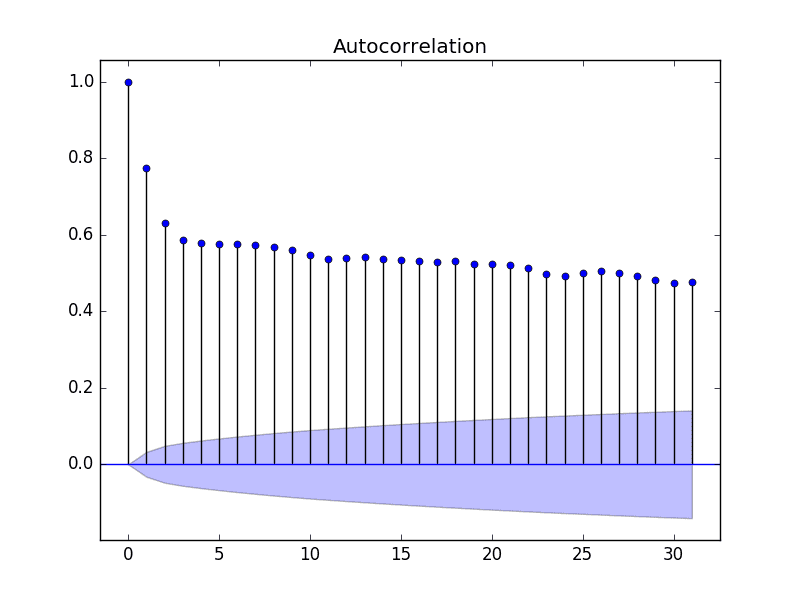
Statsmodels Autocorrelation Plot
Now that we know how to review the autocorrelation in our time series, let's expect at modeling it with an autoregression.
Before we practice that, let'due south constitute a baseline performance.
Persistence Model
Permit's say that we want to develop a model to predict the last 7 days of minimum temperatures in the dataset given all prior observations.
The simplest model that nosotros could employ to brand predictions would be to persist the last observation. We tin call this a persistence model and it provides a baseline of operation for the problem that we can use for comparison with an autoregression model.
Nosotros can develop a test harness for the problem by splitting the observations into training and examination sets, with only the last 7 observations in the dataset assigned to the examination set as "unseen" information that we wish to predict.
The predictions are made using a walk-forward validation model so that nosotros can persist the well-nigh recent observations for the next day. This means that nosotros are not making a seven-twenty-four hour period forecast, but 7 1-day forecasts.
| ane 2 3 iv v 6 vii 8 nine ten 11 12 13 fourteen 15 16 17 18 19 xx 21 22 23 24 25 26 27 28 29 30 31 | from pandas import read_csv from pandas import DataFrame from pandas import concat from matplotlib import pyplot from sklearn . metrics import mean_squared_error series = read_csv ( 'daily-min-temperatures.csv' , header = 0 , index_col = 0 ) # create lagged dataset values = DataFrame ( series . values ) dataframe = concat ( [ values . shift ( 1 ) , values ] , axis = 1 ) dataframe . columns = [ 't-ane' , 't+i' ] # split into train and examination sets Ten = dataframe . values railroad train , test = X [ one : len ( 10 ) - seven ] , 10 [ len ( X ) - seven : ] train_X , train_y = train [ : , 0 ] , train [ : , 1 ] test_X , test_y = exam [ : , 0 ] , exam [ : , 1 ] # persistence model def model_persistence ( ten ) : return 10 # walk-frontwards validation predictions = list ( ) for x in test_X : yhat = model_persistence ( 10 ) predictions . append ( yhat ) test_score = mean_squared_error ( test_y , predictions ) impress ( 'Exam MSE: %.3f' % test_score ) # plot predictions vs expected pyplot . plot ( test_y ) pyplot . plot ( predictions , color = 'red' ) pyplot . testify ( ) |
Running the example prints the mean squared error (MSE).
The value provides a baseline performance for the problem.
The expected values for the side by side 7 days are plotted (blue) compared to the predictions from the model (cerise).
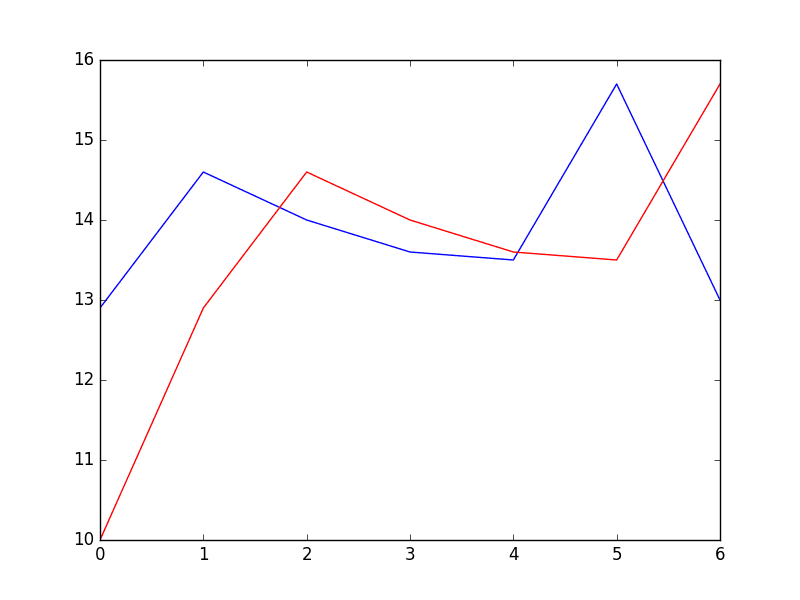
Predictions From Persistence Model
Autoregression Model
An autoregression model is a linear regression model that uses lagged variables every bit input variables.
We could calculate the linear regression model manually using the LinearRegession class in scikit-learn and manually specify the lag input variables to employ.
Alternately, the statsmodels library provides an autoregression model where you must specify an appropriate lag value and trains a linear regression model. It is provided in the AutoReg class.
We can use this model by get-go creating the model AutoReg() and then calling fit() to train it on our dataset. This returns an AutoRegResults object.
Once fit, nosotros can use the model to make a prediction by calling the predict() function for a number of observations in the futurity. This creates one 7-day forecast, which is different from the persistence example higher up.
The complete example is listed below.
| 1 2 3 four 5 6 vii eight 9 x 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | # create and evaluate a static autoregressive model from pandas import read_csv from matplotlib import pyplot from statsmodels . tsa . ar_model import AutoReg from sklearn . metrics import mean_squared_error from math import sqrt # load dataset serial = read_csv ( 'daily-min-temperatures.csv' , header = 0 , index_col = 0 , parse_dates = Truthful , clasp = Truthful ) # separate dataset X = series . values train , examination = X [ 1 : len ( 10 ) - 7 ] , 10 [ len ( X ) - 7 : ] # train autoregression model = AutoReg ( train , lags = 29 ) model_fit = model . fit ( ) print ( 'Coefficients: %due south' % model_fit . params ) # brand predictions predictions = model_fit . predict ( start = len ( train ) , end = len ( train ) + len ( test ) - 1 , dynamic = False ) for i in range ( len ( predictions ) ) : print ( 'predicted=%f, expected=%f' % ( predictions [ i ] , test [ i ] ) ) rmse = sqrt ( mean_squared_error ( test , predictions ) ) impress ( 'Test RMSE: %.3f' % rmse ) # plot results pyplot . plot ( test ) pyplot . plot ( predictions , color = 'ruby-red' ) pyplot . testify ( ) |
Running the example the list of coefficients in the trained linear regression model.
The 7 day forecast is then printed and the hateful squared error of the forecast is summarized.
| Coefficients: [ 5.57543506e-01 5.88595221e-01 -9.08257090e-02 4.82615092e-02 iv.00650265e-02 iii.93020055e-02 two.59463738e-02 4.46675960e-02 ane.27681498e-02 3.74362239e-02 -8.11700276e-04 4.79081949e-03 ane.84731397e-02 2.68908418e-02 5.75906178e-04 ii.48096415e-02 vii.40316579e-03 9.91622149e-03 3.41599123e-02 -9.11961877e-03 2.42127561e-02 ane.87870751e-02 one.21841870e-02 -ane.85534575e-02 -1.77162867e-03 1.67319894e-02 1.97615668e-02 9.83245087e-03 6.22710723e-03 -1.37732255e-03] predicted=11.871275, expected=12.900000 predicted=13.053794, expected=14.600000 predicted=13.532591, expected=xiv.000000 predicted=13.243126, expected=thirteen.600000 predicted=thirteen.091438, expected=13.500000 predicted=xiii.146989, expected=xv.700000 predicted=13.176153, expected=13.000000 Test RMSE: 1.225 |
A plot of the expected (blueish) vs the predicted values (red) is made.
The forecast does look pretty skillful (virtually 1 degree Celsius out each twenty-four hours), with big deviation on day 5.
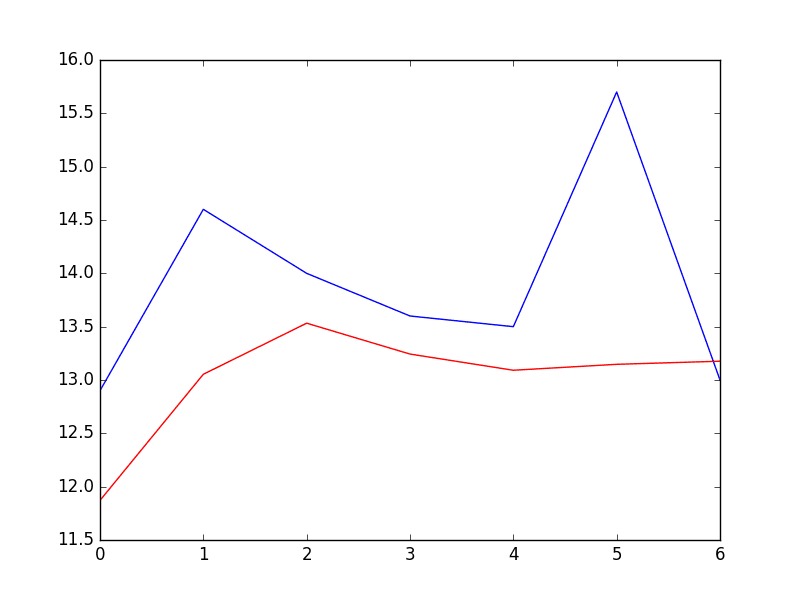
Predictions From Fixed AR Model
The statsmodels API does non make it piece of cake to update the model as new observations go available.
One mode would be to re-train the AutoReg model each 24-hour interval as new observations become available, and that may be a valid approach, if not computationally expensive.
An culling would be to use the learned coefficients and manually make predictions. This requires that the history of 29 prior observations be kept and that the coefficients be retrieved from the model and used in the regression equation to come up with new forecasts.
The coefficients are provided in an assortment with the intercept term followed past the coefficients for each lag variable starting at t-i to t-n. We just need to use them in the right order on the history of observations, equally follows:
| yhat = b0 + b1*X1 + b2*X2 ... bn*Xn |
Beneath is the complete example.
| 1 2 3 4 5 6 7 viii 9 10 eleven 12 thirteen 14 15 sixteen 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 | # create and evaluate an updated autoregressive model from pandas import read_csv from matplotlib import pyplot from statsmodels . tsa . ar_model import AutoReg from sklearn . metrics import mean_squared_error from math import sqrt # load dataset series = read_csv ( 'daily-min-temperatures.csv' , header = 0 , index_col = 0 , parse_dates = True , squeeze = True ) # split dataset X = series . values railroad train , test = Ten [ i : len ( Ten ) - seven ] , Ten [ len ( 10 ) - seven : ] # train autoregression window = 29 model = AutoReg ( train , lags = 29 ) model_fit = model . fit ( ) coef = model_fit . params # walk forward over fourth dimension steps in test history = railroad train [ len ( train ) - window : ] history = [ history [ i ] for i in range ( len ( history ) ) ] predictions = listing ( ) for t in range ( len ( test ) ) : length = len ( history ) lag = [ history [ i ] for i in range ( length - window , length ) ] yhat = coef [ 0 ] for d in range ( window ) : yhat += coef [ d + i ] * lag [ window - d - 1 ] obs = test [ t ] predictions . append ( yhat ) history . append ( obs ) print ( 'predicted=%f, expected=%f' % ( yhat , obs ) ) rmse = sqrt ( mean_squared_error ( test , predictions ) ) print ( 'Examination RMSE: %.3f' % rmse ) # plot pyplot . plot ( test ) pyplot . plot ( predictions , color = 'red' ) pyplot . prove ( ) |
Again, running the example prints the forecast and the mean squared mistake.
| predicted=11.871275, expected=12.900000 predicted=thirteen.659297, expected=14.600000 predicted=fourteen.349246, expected=xiv.000000 predicted=thirteen.427454, expected=13.600000 predicted=13.374877, expected=thirteen.500000 predicted=13.479991, expected=15.700000 predicted=14.765146, expected=13.000000 Test RMSE: i.204 |
Nosotros can see a small comeback in the forecast when comparison the error scores.
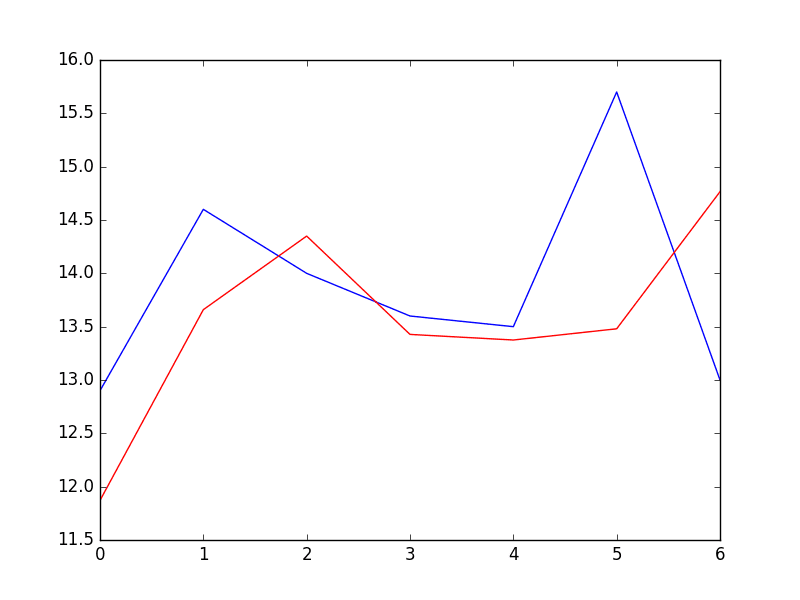
Predictions From Rolling AR Model
Further Reading
This section provides some resources if you are looking to dig deeper into autocorrelation and autoregression.
- Autocorrelation on Wikipedia
- Autoregressive model on Wikipedia
- Chapter vii – Regression-Based Models: Autocorrelation and External Information, Practical Time Series Forecasting with R: A Hands-On Guide.
- Department 4.five – Autoregressive Models, Introductory Time Series with R.
Summary
In this tutorial, you discovered how to make autoregression forecasts for time serial data using Python.
Specifically, you lot learned:
- About autocorrelation and autoregression and how they can exist used to improve understand time serial data.
- How to explore the autocorrelation in a fourth dimension series using plots and statistical tests.
- How to train an autoregression model in Python and apply it to make brusque-term and rolling forecasts.
Do y'all accept any questions about autoregression, or well-nigh this tutorial?
Ask your questions in the comments below and I will do my all-time to answer.
Want to Develop Fourth dimension Series Forecasts with Python?
Develop Your Own Forecasts in Minutes
...with only a few lines of python lawmaking
Find how in my new Ebook:
Introduction to Fourth dimension Series Forecasting With Python
It covers self-written report tutorials and end-to-terminate projects on topics like: Loading information, visualization, modeling, algorithm tuning, and much more...
Finally Bring Time Series Forecasting to
Your Own Projects
Skip the Academics. Simply Results.
See What's Within
In an Autoregressive Model How Do You Know if You Should Remove Any Variables
Source: https://machinelearningmastery.com/autoregression-models-time-series-forecasting-python/
0 Response to "In an Autoregressive Model How Do You Know if You Should Remove Any Variables"
Post a Comment